5MX47
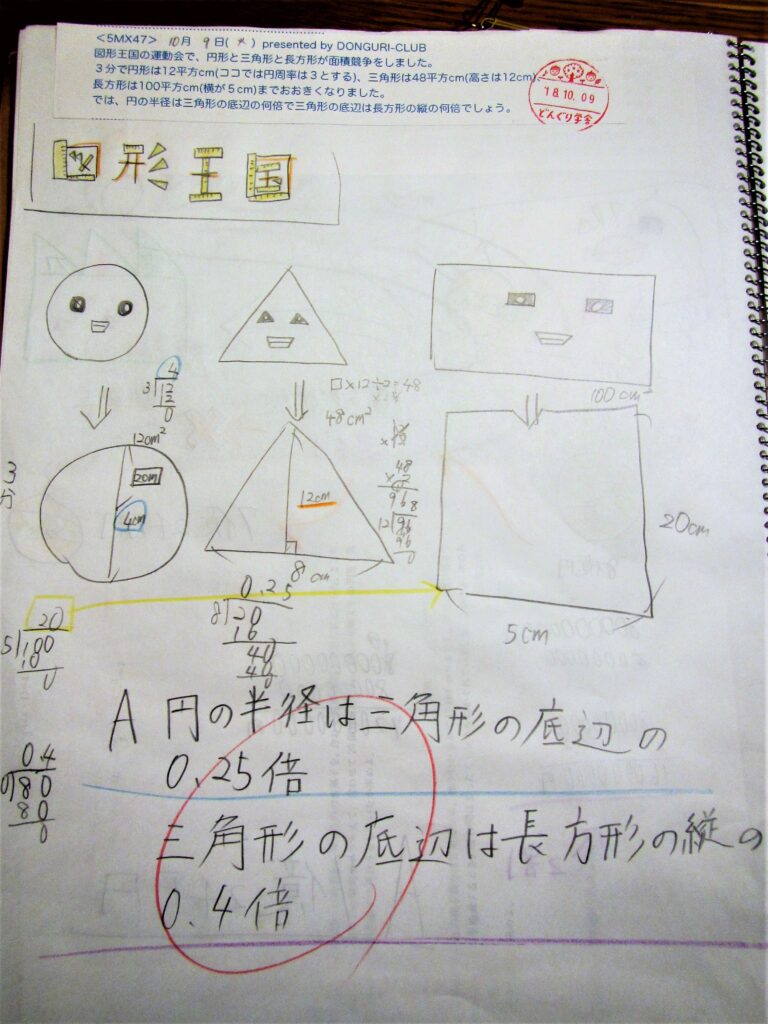
図形王国の問題です
この作品は2018に私の娘が解いたものですが、
昨日、ちょうどこの問題を解いた生徒がいました(撮影忘れました)
その子は、「1/4倍、2/5倍」と正解を出しました
小数でも分数でも同じ解答です
しっかり絵も描けて、理解しながら解いたようでしたので、他の生徒も全員教室を出た後だったのと、私の好奇心もあり、
「ところで1/4倍ってなんなんだろうねえ」と話しかけてみました
「4倍ならわかるけど、1/4倍ってなんなんだろうねえ」と
すると、ついさっきまでこの問題を思考していたその子は、
いままだその残像が脳内にあるし、クロッキー帳にはこんな風に確かに描いてあるじゃないですか、と言わんばかりの顔をして、
「そうですよね、どういう意味なんでしょう」と笑っていました
私「この問題の場合、2cmは8cmの何倍ですか?って聞いてるわけでしょ」
子「はい、そうですよね」
私「8cmは2cmの何倍ですか?って聞かれたら簡単だよねえ」
子「そうですよね、8cmは2cm4つ分なんだから、それは4倍ですよね」
私「そうだよね、じゃあ、2cmは8cmの何倍ですか、っていうことは…」
子「うーん。どういう意味なんだろう」
私は、絵を描きながら、話しました
8cmは2cmの何倍ですか?という質問も、
2cmは8cmの何倍ですか?という質問も、
同じように考えればいいんだ
8cmっていうのは、2cmをひとかたまりとすると、そのひとかたまりが何個入ってるか、っていうことだから、4個入ってる、だから4倍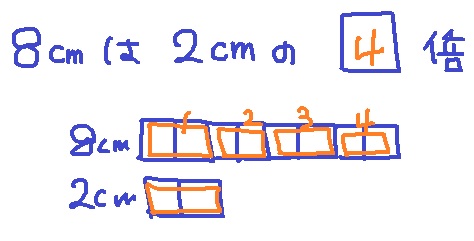
じゃあ、2cmは8cmの、って言う場合も、8cmをひとかたまりとして考えたとき、2cmはその何個分なんだろ、って考えたらいいんだよね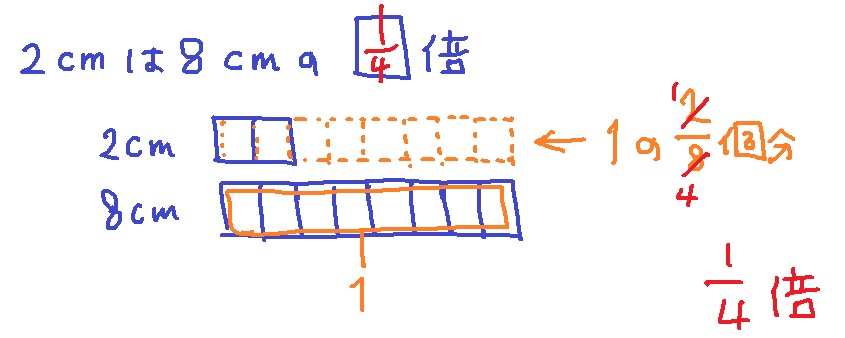
子「ああ、そういうことだ、そういうことですね」
そう、だから、8cmは20cmの何倍っていうのでも…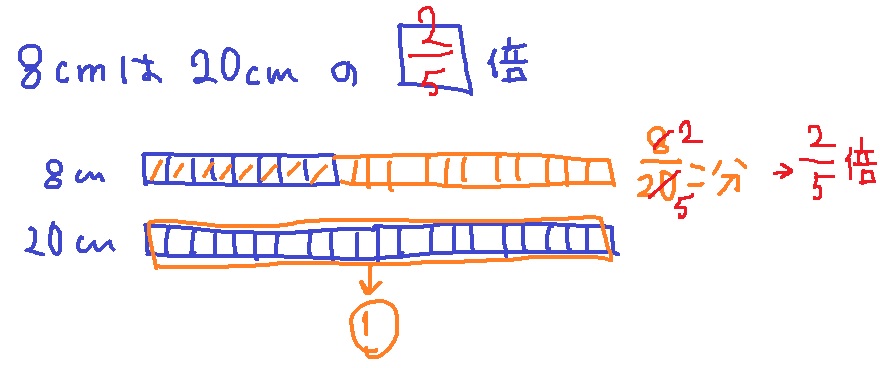
まあ、結局同じことなんだけども…
じゃあさ、じゃあさ、
分数の割り算って、割る数の分母と分子をひっくり返す、って習うでしょう?
あれ、なんでか知ってる?
私は調子づいてその子との会話を発展させていきました
子「えっと、それは、整数で割る時に、分母にその整数をかけたから、それって、整数を逆数にしてかけたことになるから…」
私「うんうん、そう習ったんだね。じゃあさ、なんで割り算は、逆数をかけるかけ算に直すのかな」
子「なんで?なんでだろう…うーん…」
私「実はさ、さっきの倍の考え方と、全く同じなんだ。そもそも、割り算って、何倍?って質問してるわけなんだよ」
子「へえ!!」
たとえば
8÷2=4は、2は8の何倍ですか?2は8の中に何個ありますか?8って2の何個分ですか?っていろんな言い方で聞けるけど、おんなじ式で求めるわけ
つまり、8÷2は、2を1としたとき、8ってそれの何個分?ってことでしょう
じゃあ、
1/3÷1/2,って割り算は言葉で言うとどんな風に表現できるか、っていうとね
さっきの8÷2と同じように考えてみると、
1/2は1/3の何倍ですか?1/2は1/3の中に何個ありますか?1/3って1/2の何個分ですか?とかってなるよね
つまり、
1/3÷1/2は、1/2を1としたとき、1/3ってそれの何個分?ってことでしょう
これね、低学年でも絵を描いて解いちゃうんだけど、今日はなんで「逆数をかけるのか」っていうところだけ考えてみるけどね、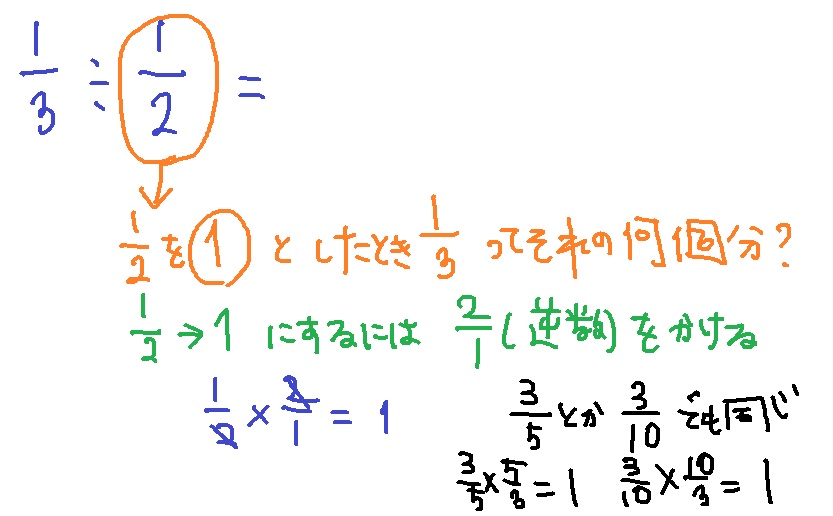
それで、1/2は逆数2/1をかければ無事1になれるわけなんだけども、
問題は1/3の方なんだよね
割り算の式の数値を変えないためにも、1/3にも巻き添えで2/1をかけないといけないの
たとえば、
6÷3=2っていう式の、わる数の3を2倍したくなっちゃったら、3が6になるよね
でも、3を2倍するんだったら、6も一緒に同じ2倍をしないと答えが変わっちゃうんだ
6を2倍すると12でしょ、
(6×2)÷(3×2)
=12÷6
=2
ね
両方同じ2倍したから答え変わらないでしょ
だから、巻き添えで、1/3の方も2/1をかけなくちゃならないの
子「じゃあ、こっち(1/2にかけるほう)じゃなくてこっち(1/3に2/1をかけてるほう)をやってるんだ」
私「そう、そういうこと」
子「なーーるーーほーーーどーーー」
そう、結果的に分数の割り算は、わる数の分母と分子を逆さまにしてかける、という作業さえすれば解けます
学校の先生もこの意味を教えているのかもしれませんが、この子のように知ろうと思わなければ話しても通過するだけでしょうし、余計混乱することを予想して最初から教えず、とにかく「ひっくり返してかける、ひっくり返してかける」ということをひたすら練習して体得させることを優先するかもしれません
結果的に「ひっくり返してかける」という作業が安定してできれば計算はできるので、問題はないのですが、長年子どもたちを見ていると、「納得して進んでいる子は理解が深く、この後の応用に強い」傾向があります
そして、この「なぜそうなるか説明せよ」は、近年の高校入試問題で全教科において、とても増えている問題なのです
そういう問題が増えると、塾などでは「記述問題対策」と銘打って、いろいろなことの説明がうまいことできるように特訓するわけですが、そんなことをしなくても、最初から納得していけば、説明せよ、と言われたときに答えることはできます
この子がそうだったように、理解して、解けているのに説明の仕方がわからないだけだったら、自分が納得していることを他者にどう伝えるのか、ということだけを練習すればいいのです
だから、
最強の勉強法は「誰かに教えること」「誰かに教えるつもりで説明を考えること」だと言われているのです
雑談の延長で、メモ書きしながらこの子と数分間話した後、次の時間の約束が入っている中学生が教室に入ってきたのでその子は帰る支度をするわけですが、その時「あの、これもらってもいいですか」と私のメモ書きを手にするのです
いやいやいや、わかるように書いてないし、汚いから…と取り返そうかと思いましたが、そうだ、じゃあ、自分でわかるように、納得できるように書き直しておくといいよ、と言うと「はい!」と言って嬉しそうに持って帰りました
割り算の計算を短文で何通りもに表現することも、
絵に描いて解いたことを誰かに説明できるほど納得することも、
どんぐりでは年長さんから当たり前のようにやっていることです
急に記述力を高める練習とか、
仕組みを理解する解説とか、する必要もありません
こちらが説明を求めなくても、子どもたちは、考える過程を絵図化することで、
自動的に理由を描いているのです
答えを早く正確に求めることではなく、考える過程を視覚イメージで再現しているのです
最も大事なのは素直さと好奇心です
学力をつけることとか、
特訓して記述力を高めることは他でもできるかもしれませんが、
子どもの心の成長を妨げず、むしろ、尊重しながらさらに高度な思考力を身につける方法を、
やっぱり私は他に知らないのです
どんぐりは家庭で、親子でできる最強学習法です
お金もかからないし、親が教えることなど何もありません
でも、もし、今、どんぐりとは無縁の子どもの学習状況だとしても、忘れないでほしいのは、
子どもが納得して進むことの大切さです
親が「子どもはきっと納得している」と思い込むのはダメです
子どもが心から納得しているかどうか、子どもの目を見てみてくださいね
とにかくやりなさい、
とにかく覚えなさい、
そんなことを言われて、自分ならどうかな、って想像してみてくださいね