
中1のDKの時間に、
そういえば「空間図形」の単元がテスト範囲だったなあ、と思い出して、
ねえねえ、円錐の表面積ってどう求めるん?と尋ねてみました
私は、自分が中学生か小学生の頃に見つけた「公式」を、ご希望なら紹介しようと思って、
わくわくしながらみんなが解くのを待っていました
すると、
思ったより早く解けたので、どうやって解いたのかなあ…とノートを覗いてみると、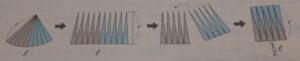
このような考え方を利用した解き方をしていました
側面の扇形を、平行四辺形に見立てて、面積を求めていました
でも、「説明して」と頼んでも、「うーん、よくわからないけどそう教わったので」と口々に言うのです
そうかあ…なるほど…と私は一瞬、言葉に詰まりました
でも、最近、とても多くなってきています
つまり、学校の授業が、少し、塾のようになってきているのです
扇形は、まんまるの円を2つの半径で切り取った形です
まんまるの円一周は360度の中心角ですが、
扇形は、中心角が30度だったり、80度だったり、半円なら180度だったり、で、様々です
面積を求めるには、中心角を求めて、それが、まんまる円のどれだけの割合なのかを考える必要があります
たとえば180度の半円の扇形ならば、それはまんまる円の1/2ですから、まんまる円の面積を1/2すればいいのです
かつて、学校ではこの求め方を紹介していました
今でも、教科書のメインのページではこの解き方で説明してあります
じゃあ、中心角はどうやったら求められるのか
試行錯誤して、生徒たちは底面の円周と、扇形の円弧の部分が同じ長さだと気づきます
…とまあ、まどろっこしいですけれど、目に見える面積の求め方、といったところでしょうか
確かに、円を切り刻んで、交互に並べたら平行四辺形のような形になります
平行四辺形の面積は底辺×高さで求められますから、切り刻んで並べ替えた片方の長さを底辺と考えると、円弧の部分の長さのちょうど半分が底辺、半径が高さ、ということになります
それで、中心角がわからなくても求められる方法、として、塾の授業で教えたり、すぐに答えが出せる公式だよ!と紹介されていたりするのは見たことがありました
教科書を見ると、確かに発展学習、的なページに載っているのです
このほか、小学校では「道のり・時間・速さ」を求めるためにこのマークを教えます
これも、昔は塾で教えるものでした
学校で教えるようになり、生徒たちもすぐこのマークをノートやプリントに書いて考えようとします
それなのに、雑談で、時速60キロの車で300キロ先まで行くのに何時間かかる?って聞いてみると、「……全然わかんない」などという子もいるのです
だって、
学校では「道のり」「時間」「速さ」に相当する言葉と数値に線を引かせ、それからこの図に当てはめて、計算式を立てさせるのです
以前紹介したこの本でも、
%がわからない学生はすぐに「みはじ」を書く傾向がある、というようなことが書いてありました
確かに、意味がわかっていれば「みはじ」を書かなくても式は立てられます
もちろん、授業の導入では、意味を話して聞かせたのだと思います
上の、円錐の側面積だって、きっと、発展学習のページを開き、みんなで考えよう、的な授業をしたのだろうと思います
でも、結局、「この式に当てはめれば答えが出るんだよ」というところまで教えたら、子どもは、それまでの途中経過になど興味を持たないでしょう
いくら、その途中経過、考える過程が大事なんだよ、と話して聞かせても、最後には完成形が、はいよ、と配られるならそれだけゲットすればいいじゃん、って思う子が多いのも必然です
人気の教育動画などを見ても、
ネットで「解き方」を探ってみても、
どれもこれも、たぶん、作っている方の能力が高いせいもあって、
まどろっこしく遠回りに考えるよりも、もっと簡単に、もっと確実に求められる方法があるんだよ、と教えてくれているものがとても多いです
いつも生徒に言うのです
全部覚えられるなら覚えればいいよ、と
便利な公式だ!便利な図だ!と思うなら、全部、間違いなく使いこなせるように正確に、しかも、整理しながら覚えておくといいさ
でも、だいたい、忘れてしまうのです
だから、こう言って質問してきます
「これってどうやるんでしたっけ?」
「これ、どうやるか忘れちゃったんですけど」
考えずに覚えたことは、こうやって「穴」になっていきます
「穴」と「穴」につながりはないので、どんどん、抜け落ちていくイメージです
考えて納得して乗り越えてきた知識には、全部つながりがあって、忘れてしまっても、他の部分がつながっていて、連鎖で思い出したり、再び考えついたりします
だから、公式を覚えるときも、必ず、納得してからにして
説明できるまで体得してから使って
と、いつも言ってきました
DKの子たちはどんぐり学舎で考える習慣を身につけてきたので、
そのまま、考え続け、納得しながら中学校の勉強も進めていけると思います
でも、私なんかよりずっと存在感のある学校の先生が、毎日会っている学校の先生が、
短絡的で効率のいい解き方を自ら教えてしまったら、
生徒たちはいつか、考える勉強ではなく、覚える勉強に慣れていくのでしょうか
いつから学校の授業は、塾みたいになっちゃったんでしょうか
全ての子をすくい上げるための秘策なんだとしたら、それは、
逆効果だと私は思います
こうやって解けばいいんじゃない?これってこういう意味なんじゃない?
導入授業でよくおこなわれる、活発な議論で授業が進んでいる、と思っている先生たちもいるでしょうけれど、
たぶん、教室の半分くらいの生徒、もしかしたらそれ以上の生徒たちが、議論に加わっていません
書け、と言われたことを書き、
読め、と言われたことを読み、
何か指示されるまで脳を動かさないタイプです
そして、結論として出てきた公式を、丁寧にノートに書き、宿題をするときはその公式に当てはめて解いていきます
テストになると、公式を思い出せず、解けないし、少し問題にひねりがあれば、どこをどう公式に当てはめたらよいのかも、わからなくなってしまいます
先日、DKではない中学生たちの勉強を見ていたら、学校の宿題で、理科の公式や用語をひたすら書かされているのを見ました
書いている言葉の意味を問うと、「わかりません…」と言っていました
ちなみに、宿題で英単語の練習をしている子に「なんて読むの?」と聞いても、「わかりません…」と言っていました
わからないまま書くことに、慣れきっている様子でした
それは、小学校時代から始まっていますよね
いくら教育動画が流行しても、いくら高学歴の学生さんが自分のノート術や勉強法を紹介して流行させても、子どもたちがどうやって知識を獲得し、自分のものにしていくのか、思考力とは何なのか、という部分を無視していては、現状は何も変わりません
短絡的で、効率のいい解き方は、解きながら自分で考え、思いつくものです
誰かに教えてもらうものではありません
誰かと一緒に勉強していて、一緒に考えつくこともあるでしょう
そんな議論ができる仲間がいたら、三人寄れば文殊の知恵状態だったら、最強でしょう
私が子どもの頃に見つけた円錐の表面積の求め方は、
「もう(平行四辺形で求める方法を)知ってるから不要」という態度が見えたので、教えませんでした
実はもっともっと速い方法があるんだけどね~
覚えるだけじゃ意味がないから、教えません
教室のあちこちに、ヒントは散らばっているけれどね
でも、彼らなら、いつか見つけだす
最強のどんぐりっこたちですから
学校では、塾みたいに、速く簡単に答えが出る方法なんて教えなくていいし、
速く簡単に答えが出せる子が評価されるようなテストなんかしなくていい
もっともっと、大切なことを、授業が毎日あるなら教えられるのに…
簡単に教えられることは、簡単に忘れられてしまいます
スマホでググった内容を、すぐに忘れてしまうようにね
魚を釣ってあげないで、釣り方を教えてあげてください、って、
メッセージを送っているんですけどね…
なかなか伝わらないものです